Relations between slim and thin disks
at low mass accretion rates
Michal Bursa
Use left and right arrows to move between slides.
Spin measurements from continuum fitting
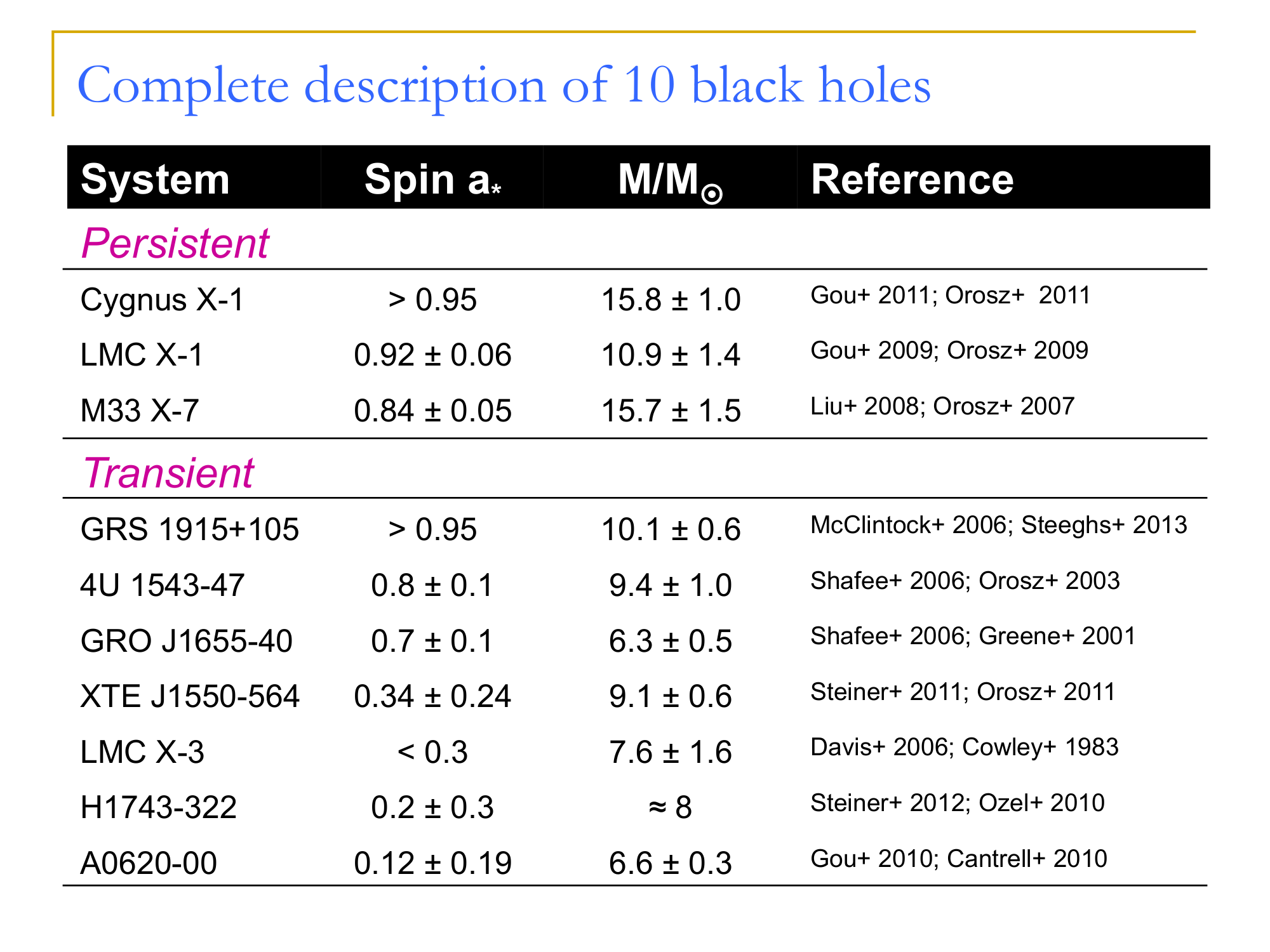
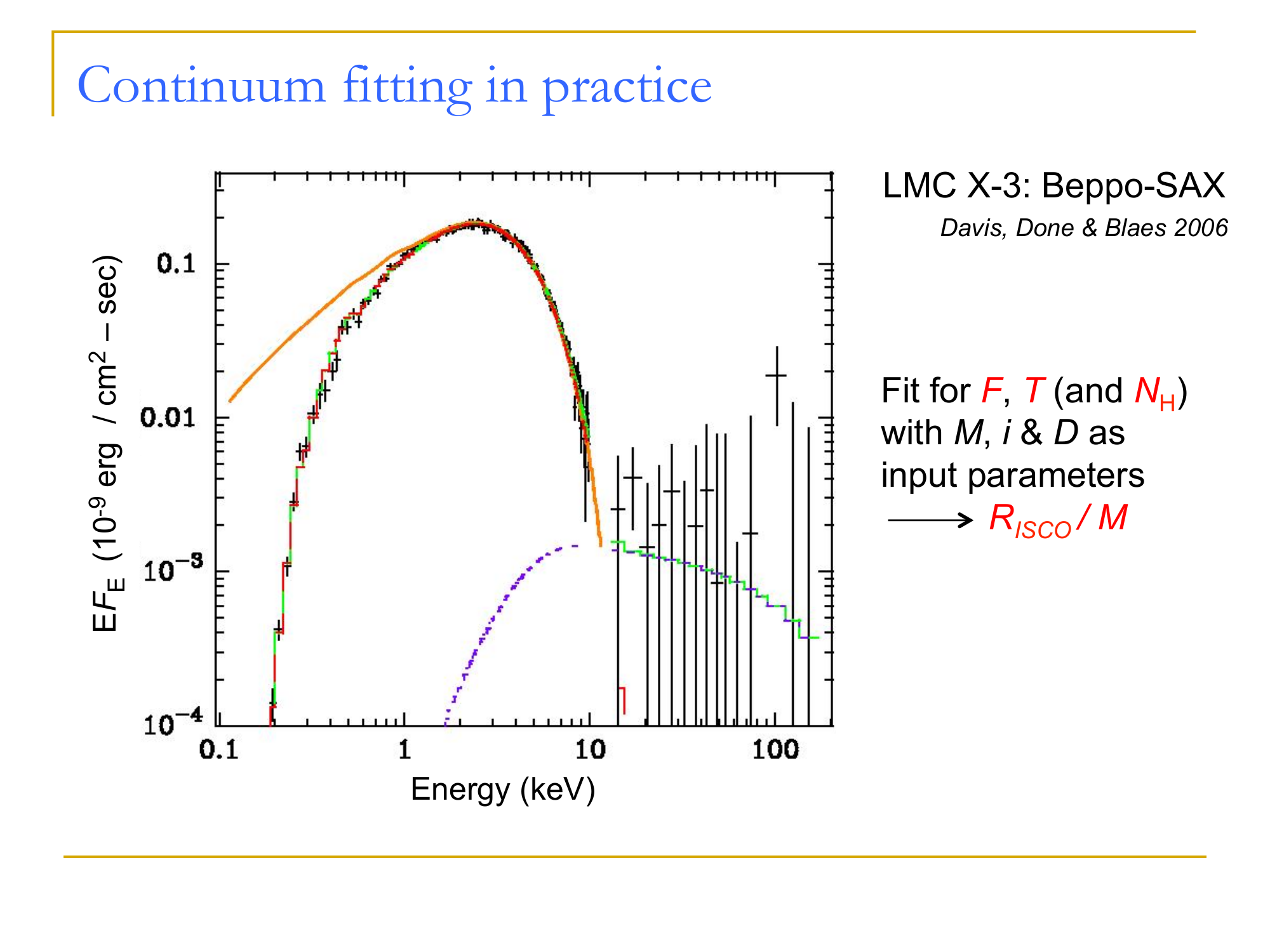
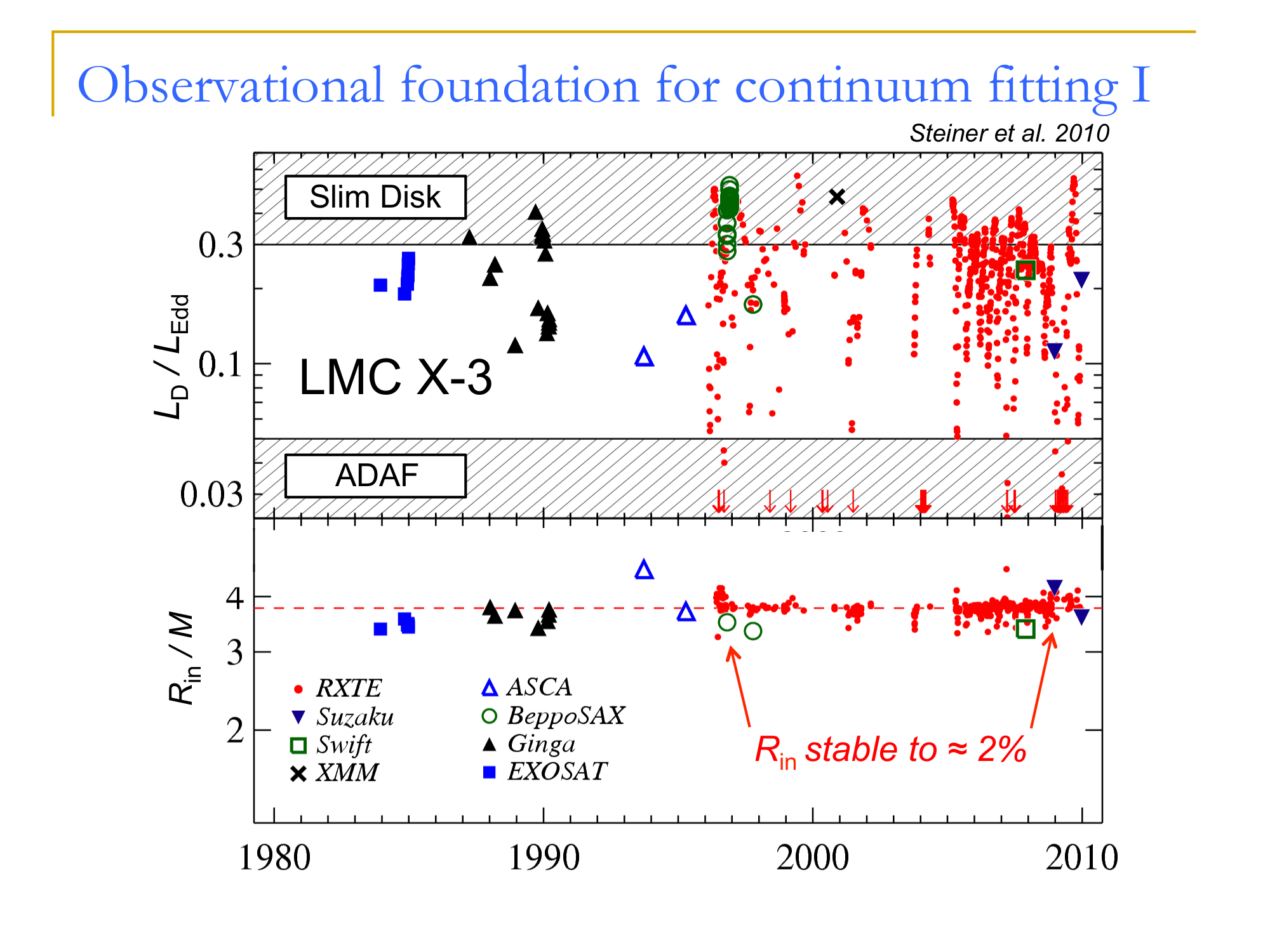
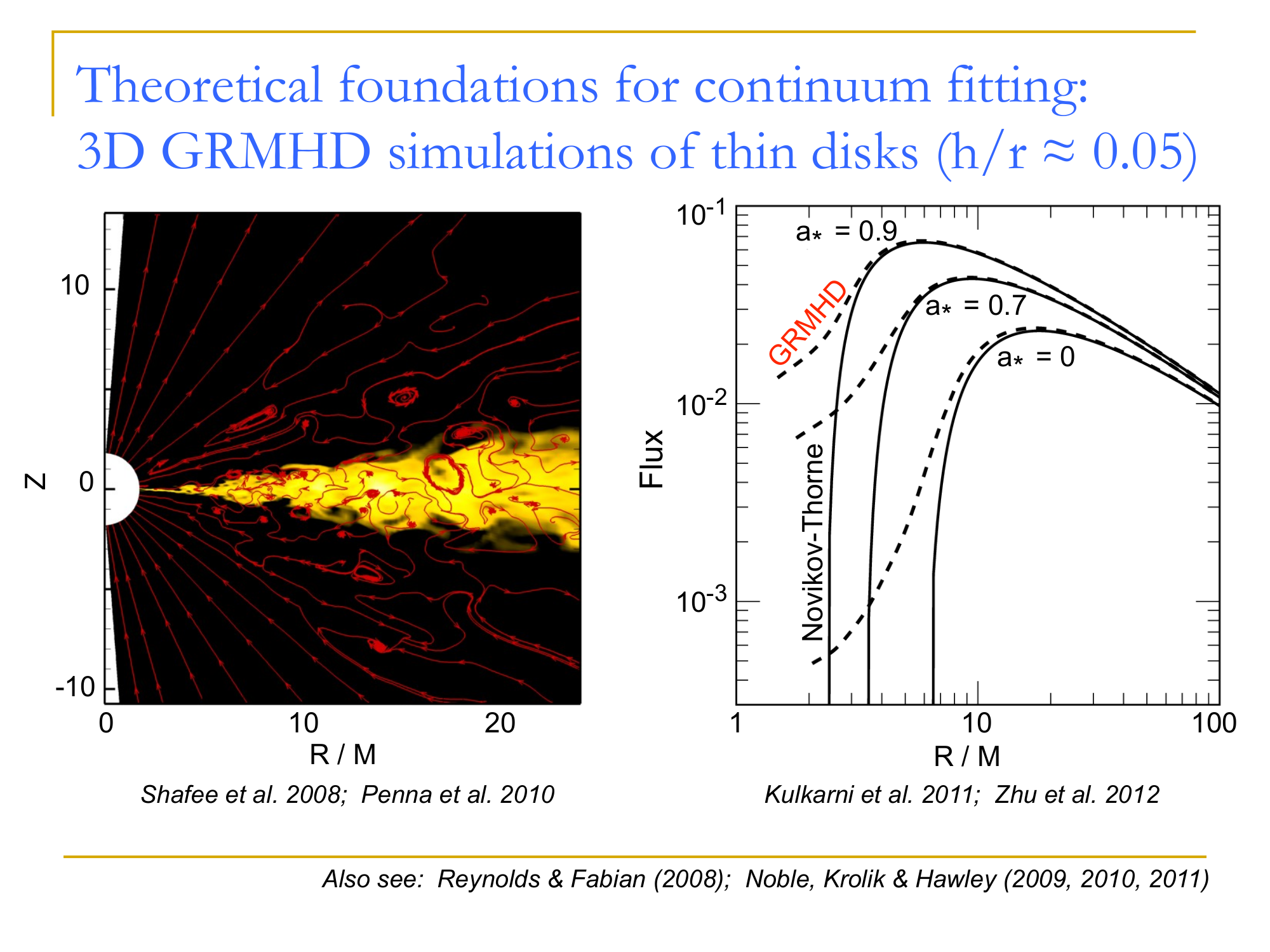
Credit: R. Narayan, J. McClintock
Spin measurements from continuum fitting
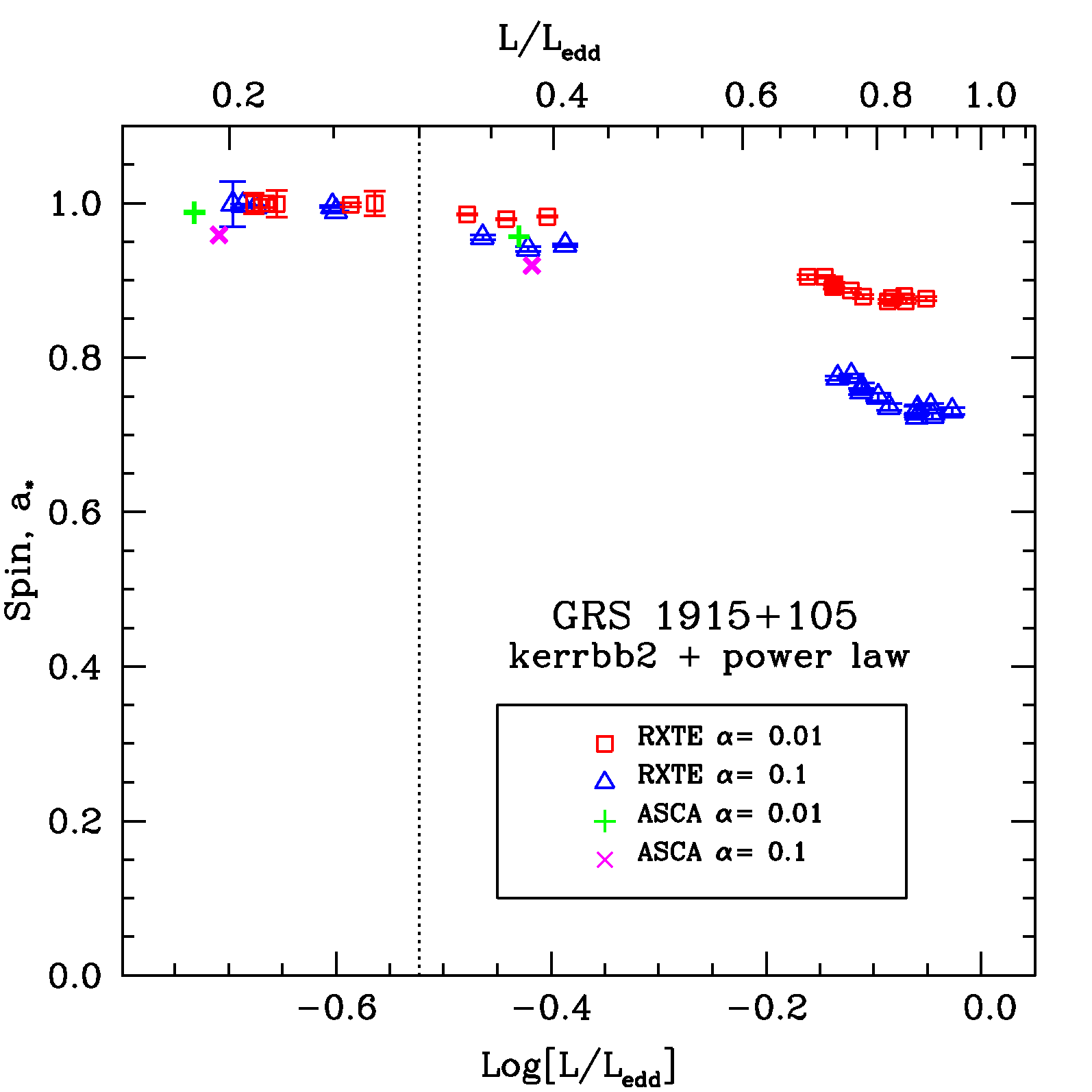
(Shafee; Steiner)
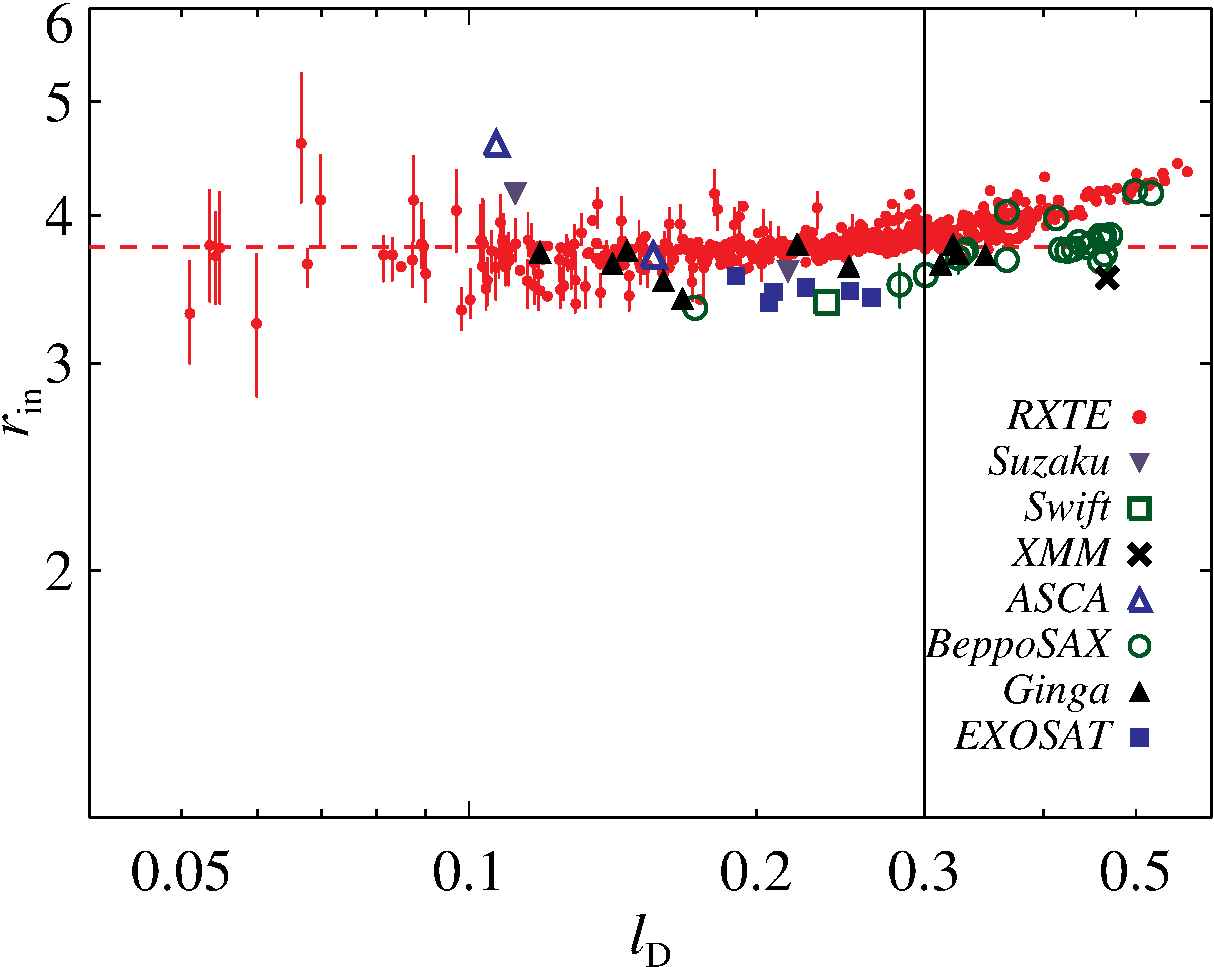
Continuum fitting with slim disks

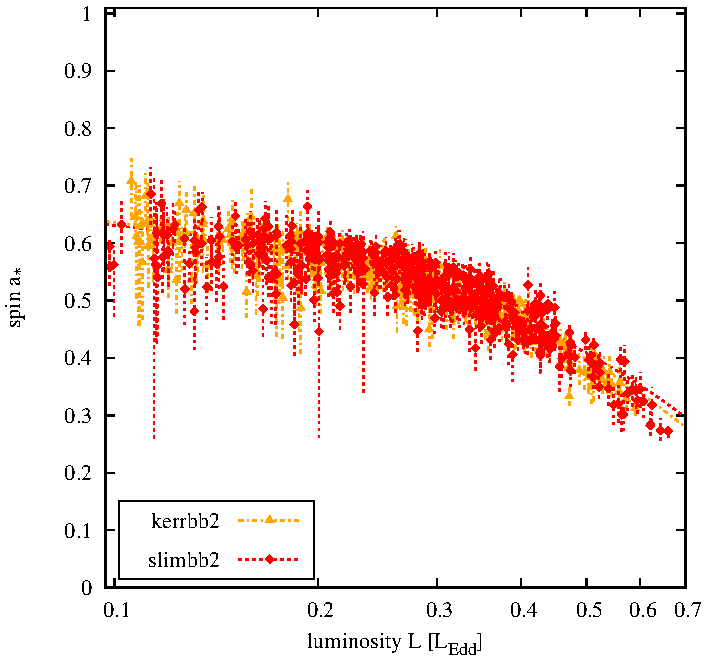
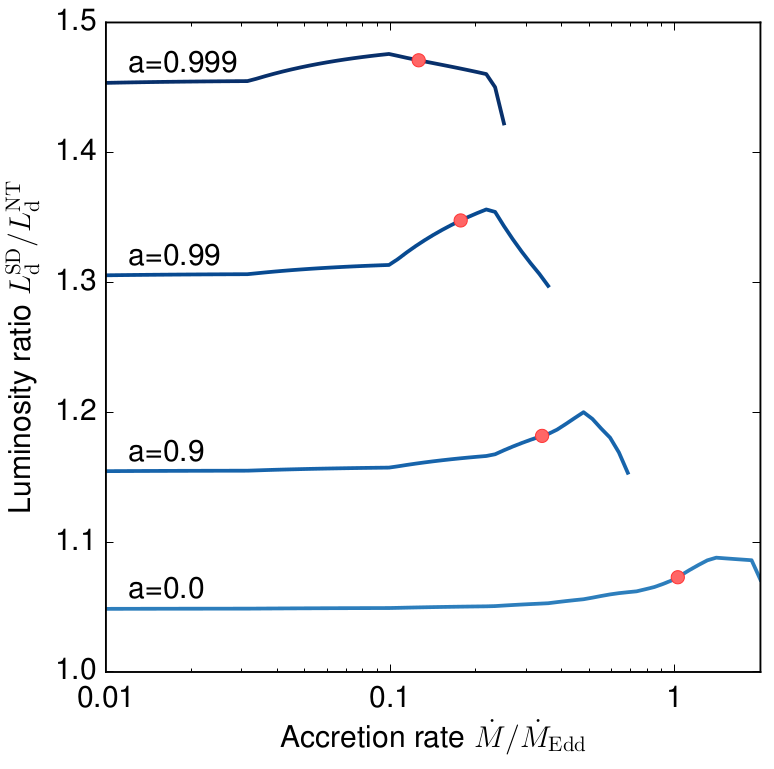
Low mass accretion rate limit of slim disk
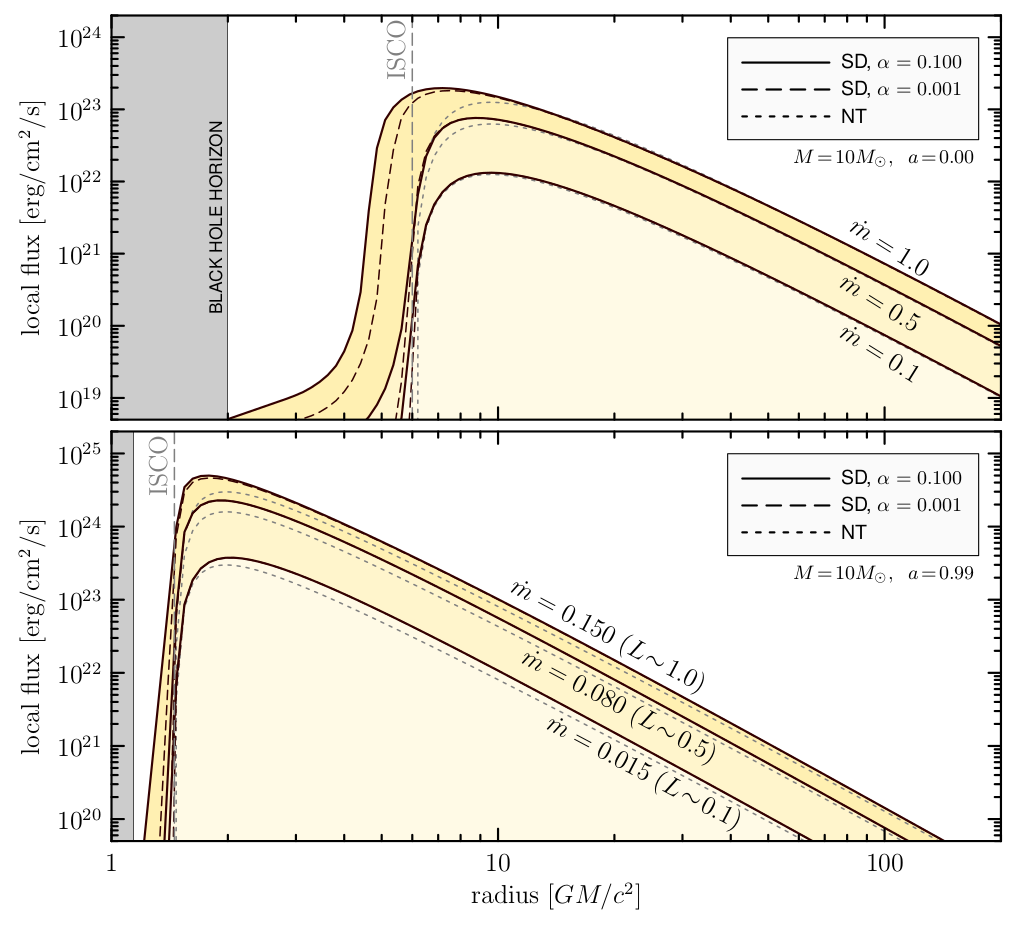
Motivation

Slim and thin disks should coincide at the low $\dot M$.
In practice, there are up to 50% different.
OPTION 1: Solve slim disk equation with the term accounting for the angular momentum transport by radiation.
OPTION 2: Solve thin disk equation without the term accounting for the angular momentum transport by radiation and make some arguments about slim disks.
Standard disk equations I.
| Total torque: | $ G(R) = 2\,\pi\,R \; \nu\,\Sigma\,R^2\,\Omega^\prime $ |
| Net torque on a ring: | $ G(R+dR) - G(R) = \cfrac{\partial G}{\partial R}\,dR $ |
| Torque caries out work: | $ \Omega\,\cfrac{\partial G}{\partial R}\,dR = \left[ \color{blue}{\cfrac{\partial}{\partial R}(G\Omega)} - \color{red}{G\Omega^\prime} \right]\,dR $ $\color{blue}{\partial(G\Omega)/{\partial R}}$: rate of flow of rotational energy, $\color{red}{G\Omega^\prime}$: local rate of loss of mechanical energy |
| Local rate of energy release: (per unit time and area) |
$ D(R) = \cfrac{G\,\Omega^\prime dR}{2\cdot 2\pi\,R\,dR} = \cfrac{G\,\Omega^\prime}{4\pi R} = \cfrac{9}{8}\nu\,\Sigma\,\cfrac{G\,M}{R^3}$
$ D(R) = \cfrac{3\,G\,M\,\dot{M}}{8\,\pi\,R^3} \left[ 1 - \left(\cfrac{R_{\rm in}}{R}\right)^{1/2} \right] $ (radiative cooling flux) |
Standard disk equations II.
Potential energy
$$ \cfrac{G\,M\,\dot{M}}{R} = \begin{cases} \frac{1}{2}GM\dot{M}R^{-1} = \frac{1}{2}\dot{M}\Omega^2R^2=\frac12\dot{M}v^2 & \text{(rotational energy)}, \\[1em] \frac{1}{2}GM\dot{M}R^{-1} & \text{(gravitational binding energy)}, \\ \end{cases}$$
Total luminosity
$$ L = \int_{R_{\rm in}}^\infty D(R)\,2\pi\,R\,dR = \cfrac{GM\dot{M}}{2\,R_{\rm in}}$$
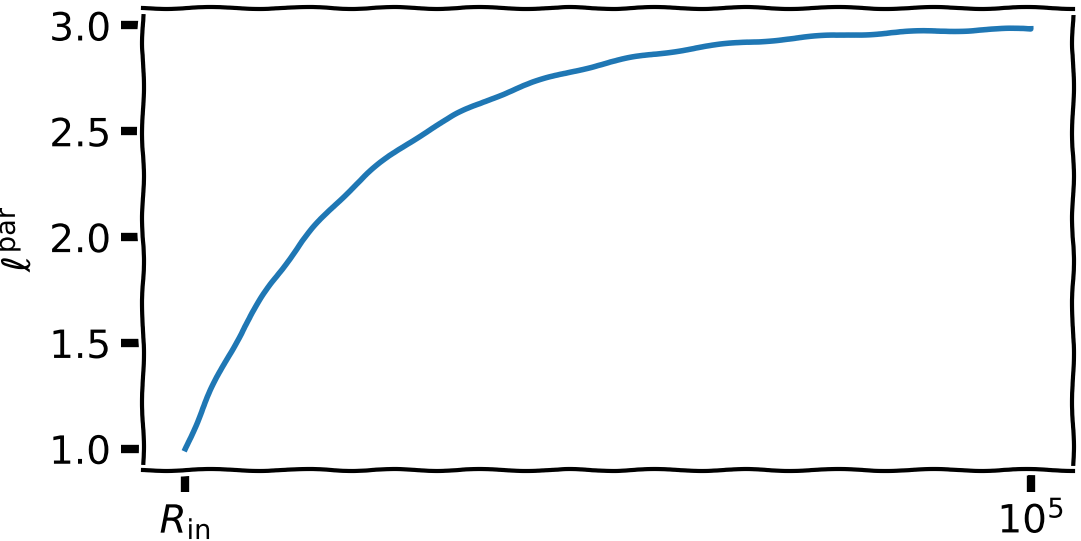
Partial luminosity
$$ L^{par}(r) = \int_{r}^\infty D(R)\,2\pi\,R\,dR = \cfrac{3GM\dot{M}}{2} \left[\cfrac{1}{r} - \cfrac23\left(\cfrac{R_{\rm in}}{r}\right)^{1/2} \right]$$ (partial luminosity from only the part of the disk with radius from $r\!>\!R_{\rm in}$ to infinity)
Standard disk equations III.
Partial luminosity
$$ \ell^{par}(R) = \cfrac{L^{par}(R)}{\frac12 GM\dot{M}R^{-1}} = 3 - 2\sqrt{\cfrac{R_{\rm in}}{R}} $$ (partial luminosity from only the part of the disk with radius from $r\!>\!R_{\rm in}$ to infinity)
Standard disk equations IV.
Energy release from a ring
$$ 2 \times 2\pi R\;D(R)\; dR = \cfrac{3GM\dot{M}}{2R^2}\left[1-\left(\cfrac{R_{\rm in}}{R}\right)^{1/2}\right]\,dR = \cfrac{GM\dot{M}}{R^2}\left[\color{red}{\cfrac{1}{2}} + \color{blue}{1-\cfrac32\left(\cfrac{R_{\rm in}}{R}\right)^{1/2}}\right]\,dR$$
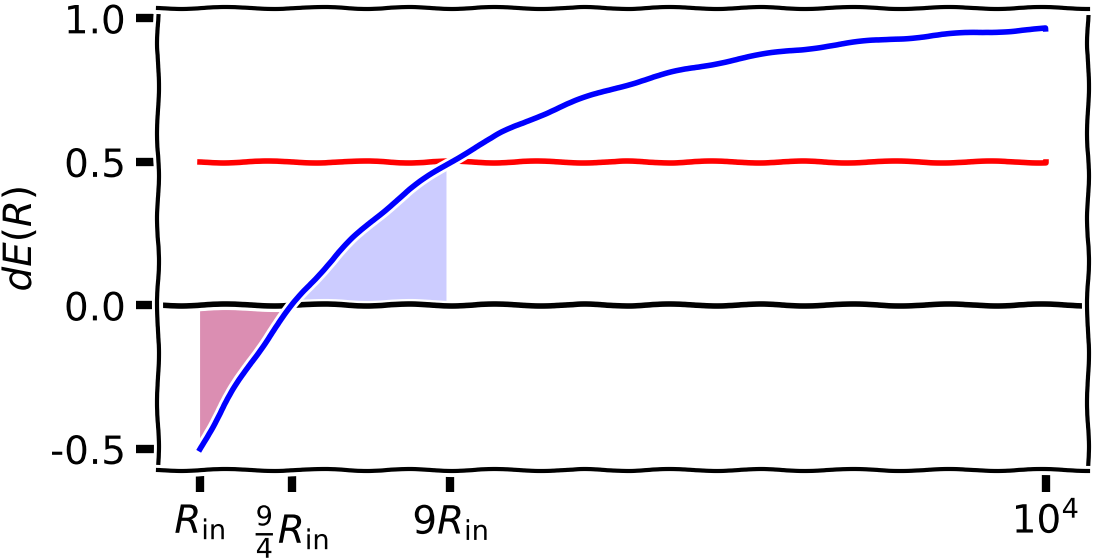
$R \gg R_{\rm in}$: loss of E due to viscous forces is twice the loss of binding energy
$R<\tfrac{9}{4}R_{\rm in}$: higher binding energy than energy loss through radiation
Relativistic thin disk
$$ \dot{M} = - 2\pi\,R\,\Sigma\,v^{\scriptscriptstyle R} $$
$$ R\,\Sigma\,v^{\scriptscriptstyle R}\,R^2\,\Omega = \cfrac{G}{2\pi} + \text{const.} $$
$$ \downarrow $$
$$ \dot{M}\left(\ell - \ell_{\rm in}\right) = G $$
(non-relativistic, integrated)
$$ \left(-\cfrac{\dot{M}L}{2\pi} + R^2\color{gray}{\mathcal{\cfrac{B}{G^{1/2}}D}}\,W\right)_{,\,r} + 2LF = 0$$
(relativistic, differential)
Relativistic thin disk - solution
$$ (E - \Omega w)_{,r} = fE $$ $$ (L - w)_{,r} = fL $$ $$ w = \cfrac{E-\Omega L}{-\Omega_{,r}}f $$ $$ \cfrac{(E-\Omega L)^2}{-\Omega_{,r}}f(r) = \int_{r_{\rm ms}}^r (E-\Omega L)L_{,r}\,dr $$ $$ f(r) = \cfrac{3}{2} \cfrac{1}{r(r^{3/2}-3r^{1/2} + 2a)} \left[r^{1/2} \, - \, r_{\rm ms}^{1/2} \, - \, \cfrac{3}{4}a\log\left(\cfrac{r}{r_{\rm ms}}\right) \, - \, \ldots \right] $$ (Page & Thorne, 1974)
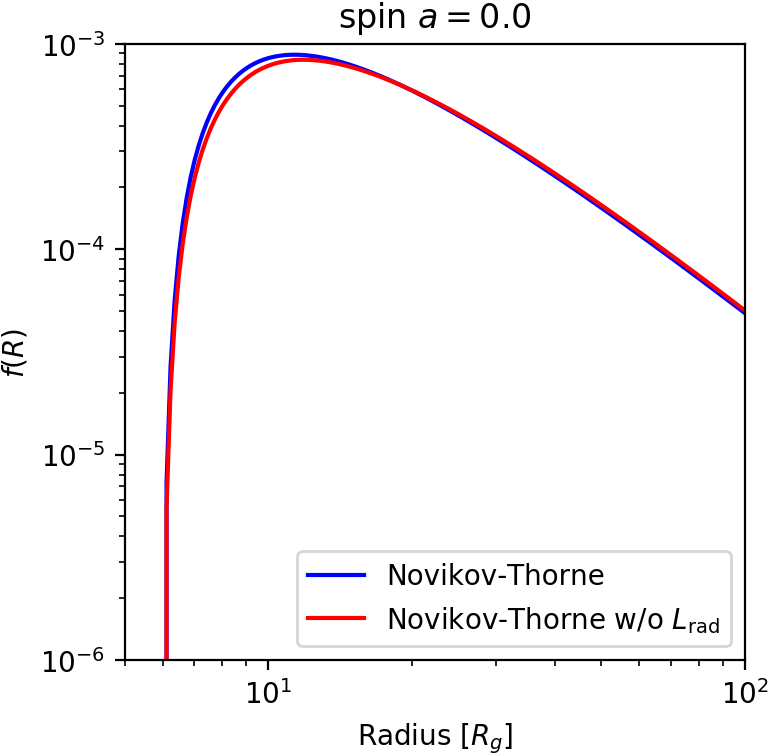
Relativistic thin disk - no L removed by radiation
$$ (E - \Omega w)_{,r} = fE $$ $$ \hspace{8em}(L - w)_{,r} = \color{red}{0} \quad \color{gray}{\text{(previously $fL$)}} \, $$ $$ w = \cfrac{E\color{lightgray}{-\Omega L}}{-\Omega_{,r}}f $$ $$ $$ $$ f(r) = \cfrac{L_{\rm in}-L}{E}\,\Omega_{,r} $$
Relativistic thin disk - no L removed by radiation
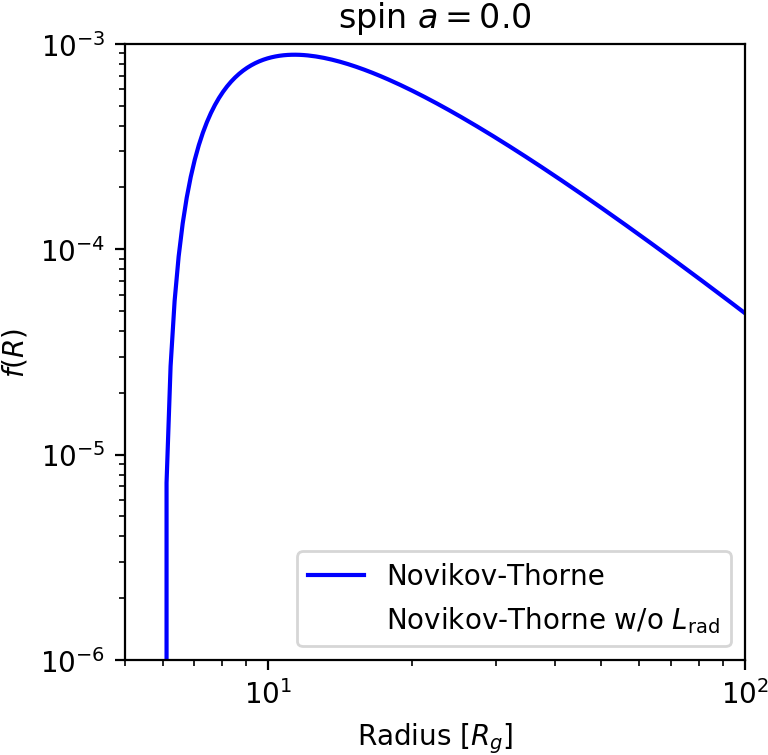
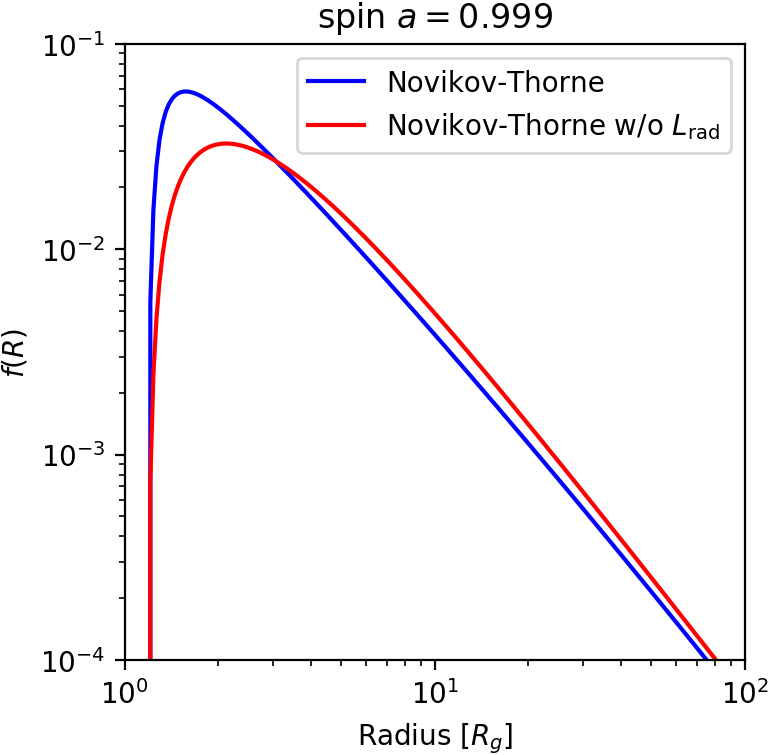
Relativistic thin disk - no L removed by radiation

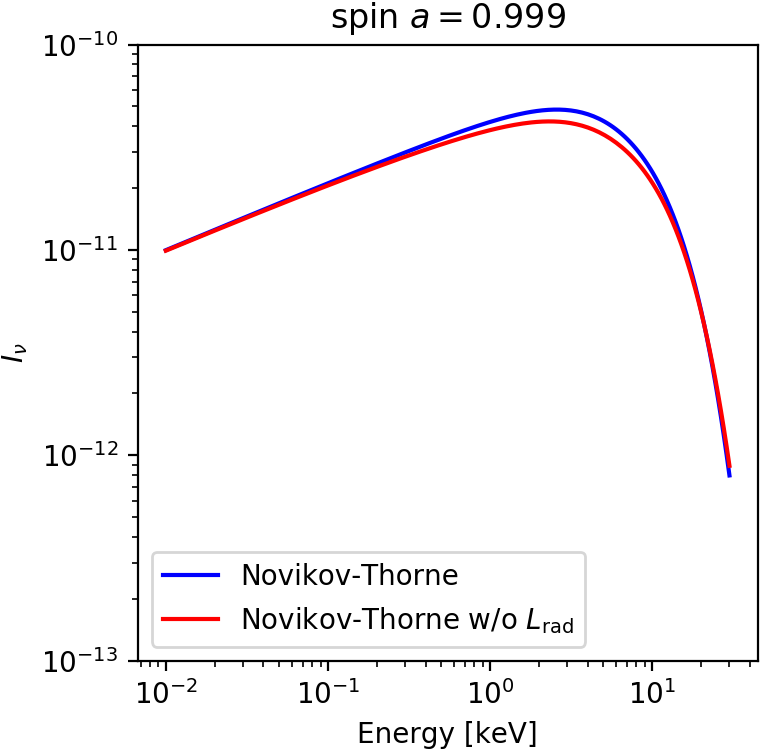
Relativistic thin disk - spectra
Slim disk - no L removed by radiation
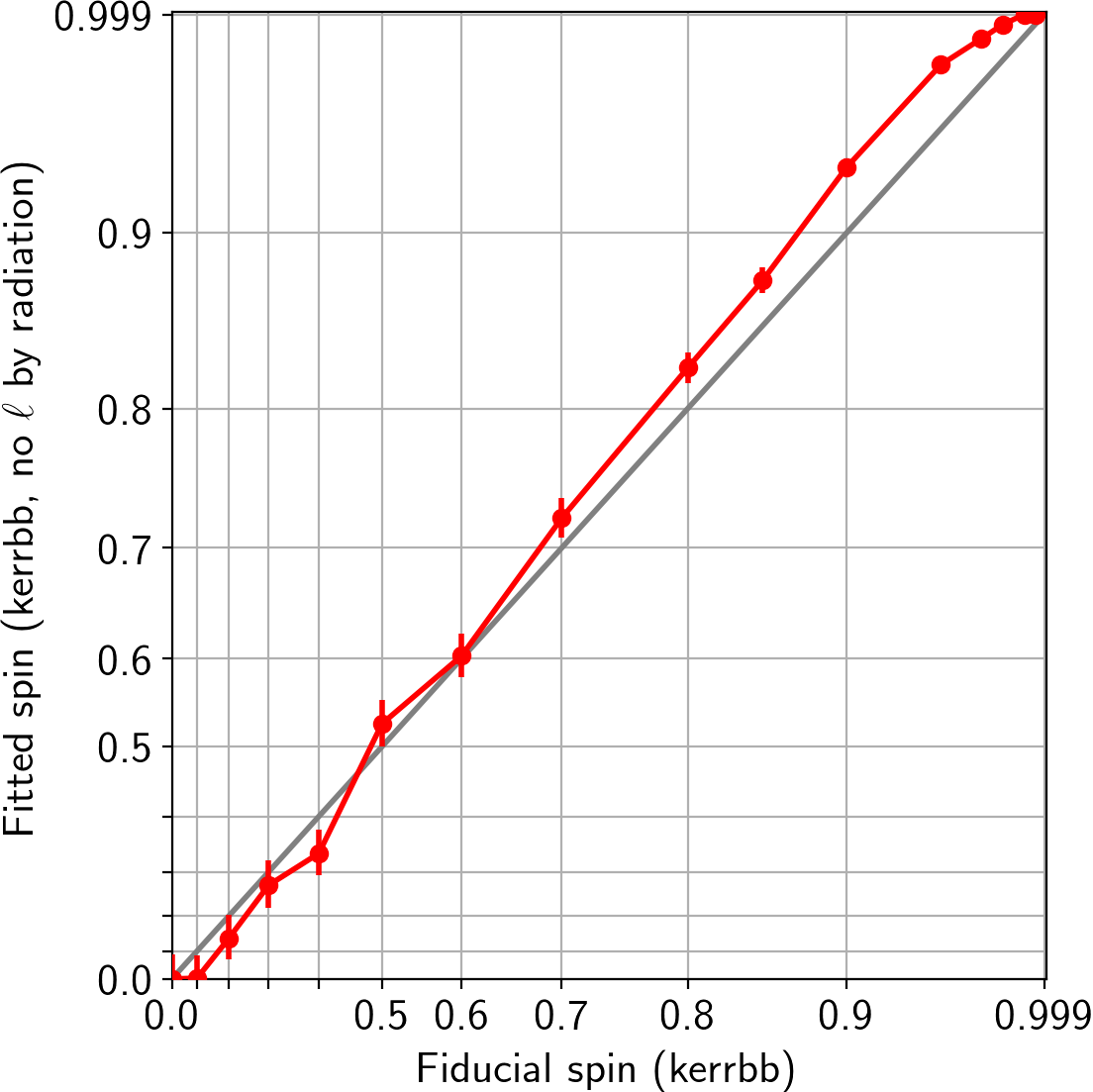
- simulated data for NT model including ang. mom. transfer by photons
- fitted with same model without accounting for ang. mom. transfer by photons
- 25ks XMM/Newton data for a source at
$D$=$10\,{\rm kpc}$, $M$=$10\,M_\odot$, $i$=$66^\circ$
Recovered spin is higher
than the fiducial one.
Slim disk - no L removed by radiation
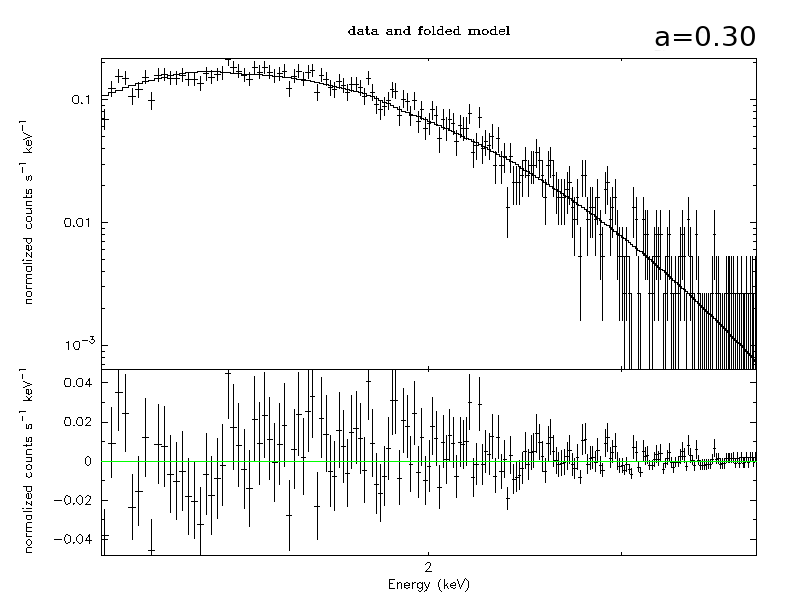
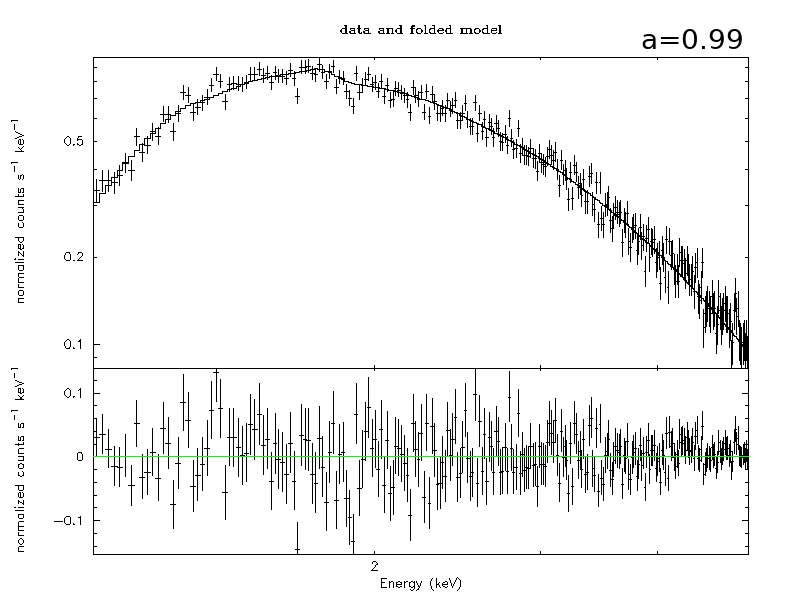
Slim disk - no L removed by radiation
thin disk:
$$ \left(-\cfrac{\dot{M}L}{2\pi} + R^2\color{gray}{\mathcal{\cfrac{B}{G^{1/2}}D}}\,W\right)_{,\,r} + 2LF = 0$$
slim disk:
$$ -\cfrac{\dot{M}}{2\pi}\cfrac{dL}{dR} - \cfrac{1}{R}\cfrac{d}{dR}\left(\Sigma\,\nu\,A^{3/2}\cfrac{\Delta^{1/2}\gamma^3}{R^4}\cfrac{d\Omega}{dR}\right) + 2FL = 0$$
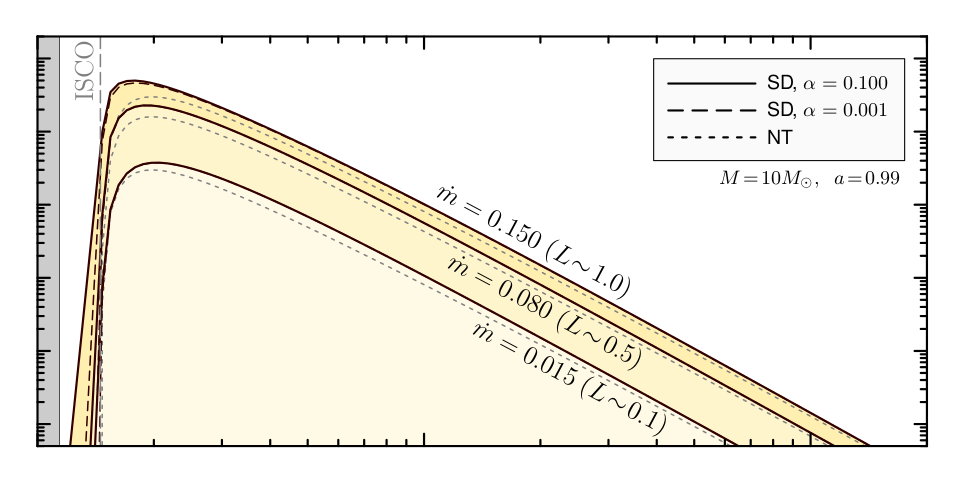
Slim disks with L removed by radiation
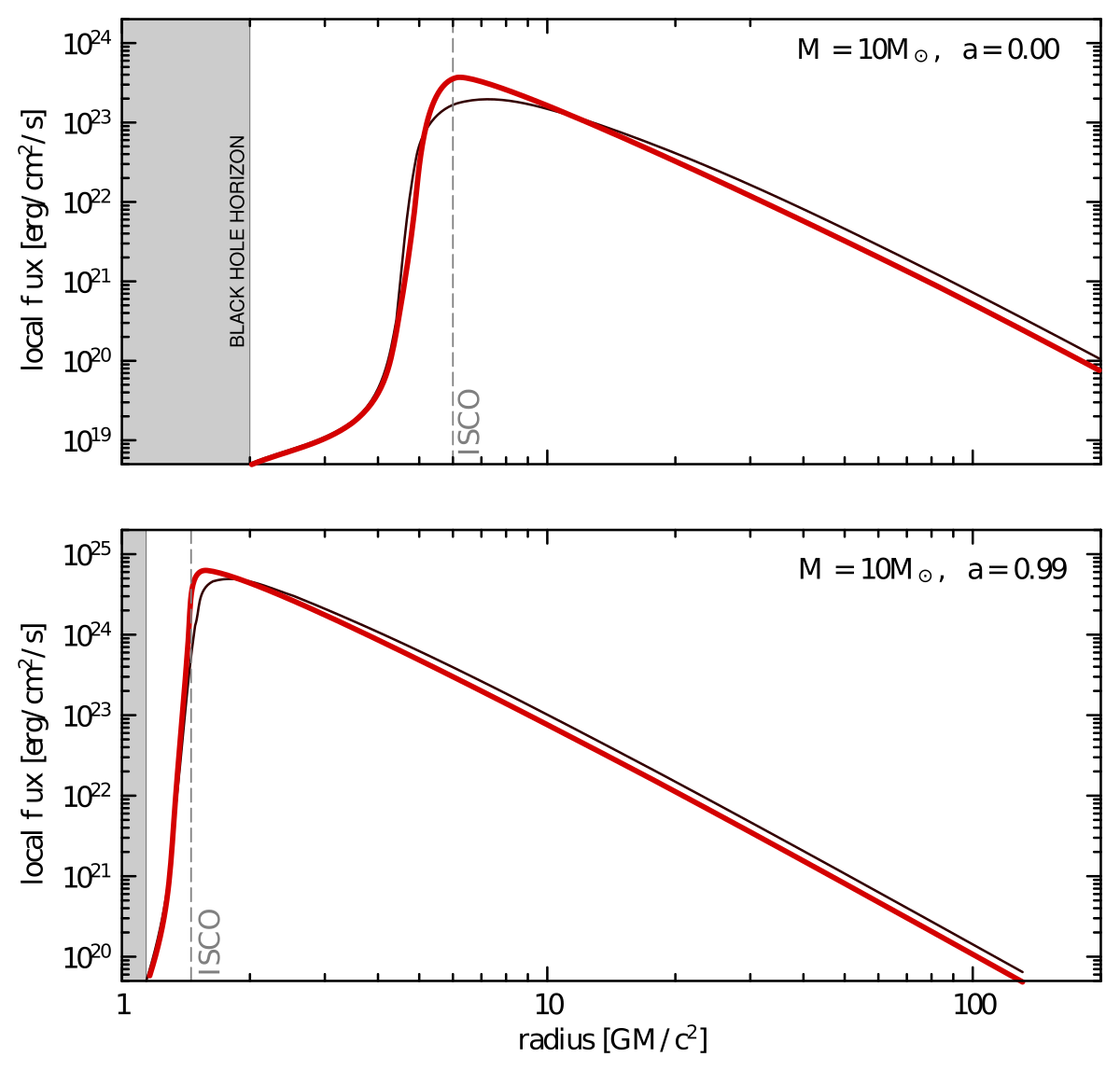
Slim disk solutions with L transported by radiation will (guess) make sharper flux peak and will have slightly lower normalization.
Key question: how does this effect depend on $\dot{M}$ (luminosity)?
Summary
In application of the slim disk model, one should be aware of:
- $L/L_{\rm Edd}<0.3$: current relativistic slim disk model does not include the effect of $L$ transport by radiation, which leads to overestimation of inferred BH spins
- $L/L_{\rm Edd}>0.3$: mass losses throughout the disk become important and potentially alter the solutions substantially